屏幕空间误差

问题

怎样判断一个 LOD 绘制结果是否会使场景看起来更好？一个简单的思路就是利用相机到被观察瓦片的距离来判断，这个距离超过指定的阈值时，就渲染下一级的瓦片。我当初写渲染引擎的时候就是这么干的，于是就有了下面这段憨批代码：

const i = MathUtil.rayIntersectEllipsoid(
  cameraPos,
  cameraPosSquared,
  normalDir,
  Ellipsoid.Wgs84.oneOverRadiiSquared
);
const h = i.near;

// ! It's ugly but useful!
if (h <= 100) {
  this._level = 19;
} else if (h <= 300) {
  this._level = 18;
} 
...
} else if (h <= 11900000) {
  this._level = 3;
} else {
  this._level = 2;
}

来解释一下这段代码，它是使用光追的方法，结合当前相机的位置和椭球体的参数得到视线与椭球体的远近交点(如果相交的话)，我们将与近交点的距离作为 h 来进行判断。这段代码虽然丑陋，但是有用(虽然效果不好)。实际上有更好的判断方式，那就是利用屏幕空间误差(ScreenSpaceError, SSE )，下面介绍 SSE 的概念，计算方式和使用效果。

概念

首先在介绍 SSE 之前，还需要引入一个叫做几何度量误差(Geometric Error, GE )的概念，其可以定义为：计算机图形图像学领域中用来描述计算机绘制的近似几何模型与理想数学模型之间近似程度的一种度量误差。而 SSE 时几何度量误差在三维渲染管线处理后最终呈现在屏幕上的一种表现形式，下面有一个图¹能很好地表明两者之间的关系。它是希望通过不断地增加多边形的边数来近似的绘制圆，实际上在不断近似成圆的过程就可以看做是 HLOD 的由非精细到精细的切换过程：

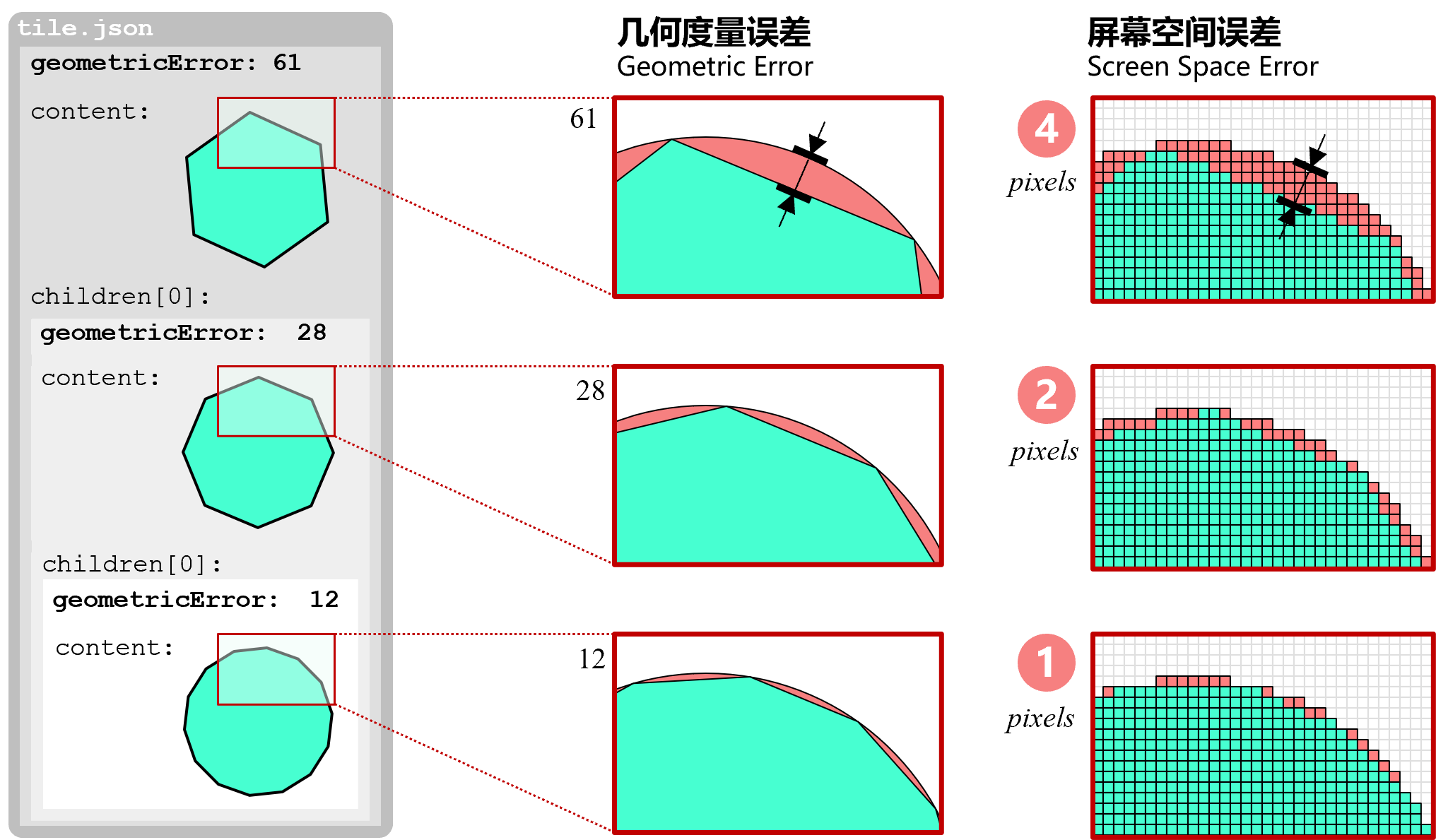
GE vs SSE

计算

想要精确计算 SSE 是有一定难度的，但是可以高效的估算出来。也就是说，当我们拉近距离时，如果现有模型计算出来的 SSE 超过了某一阈值，那么我们就应该加载下一级(更精细)的模型了。这里所说的某一阈值在 Cesium 中称为最大屏幕空间误差(maximumScreenSpaceError, MSSE )。同样的，当我们拉远距离时，就可以选择加载粗糙的模型来减少渲染压力。在这里要强调的是， MSSE 一经设定在每个层级都是固定的(可以在每一帧里面人为的修改)。下面我们具体来看 SSE 是如何计算的，最后我们会得到一个公式，其中相机距模型的距离 d 和模型的几何误差 GE 是影响 SSE 的关键因素：

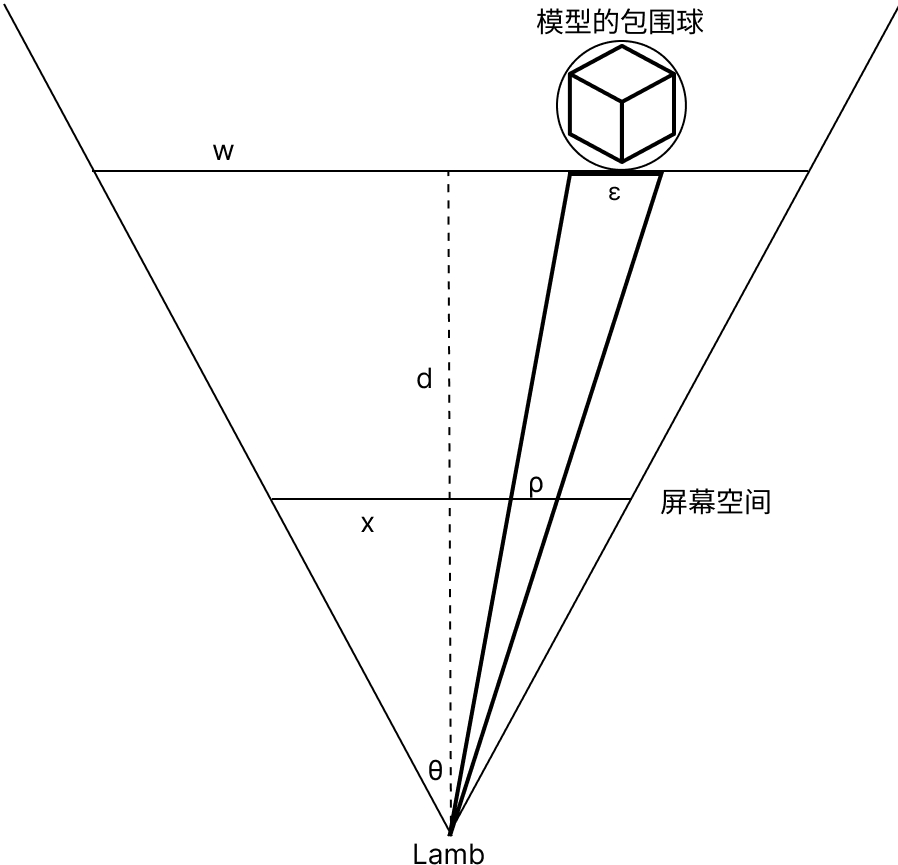
SSE Infer

在上图，物体沿视点方向距离观察者距离为 d ，视锥体宽度为 w ，显示器横向(纵向同理)分辨率为 x 像素，视场角为 θ ，当前模型对应的的几何误差为 ε 。以上变量的数值都已知(切模型时，对应层级模型的 GE 已经确定，在对应的 json 文件中有记录)，那么该模型对应的屏幕空间误差 ρ 为多少？

从图中可见， ρ 和 ε 成正比，可得：

$\frac{ε} {w} = \frac{ρ} {x}$

简单的移项后可以发现只有 w 不能直接得到，但是视锥体的宽度可以根据距离 d 计算出来：

$w = 2dtan\frac{θ} {2}$

这里的 d 就不像一开始那样可以使用光追求射线和椭球体的交点了(之前求得是椭球体上的表面点)。假设包围球的中心点为 c ，半径为 r ，在视点方向 v 上距离包围球最近点的距离 d 为：

$d = (c - vierer) · v - r$

将 w 代入即可求得当前模型在当前状态下的 SSE :

$ρ = \frac{εx} {2dtan\frac{θ} {2}}$

其实上面的内容就是 Cesium 的作者写的，我只是加上自己的理解搬运过来的，最后我们看一下现在 Cesium 在代码里面 SSE 的计算公式：

1	error = (geometricError * height) / (distance * sseDenominator);

可以发现他们用了 height ，就是 canvas 标签对应的像素高度(实际上没这么简单)， sseDenominator 和上面的公式对比也很容易能明白如何计算。到这里 SSE 如何计算我们就已经很清楚了，可以发现其的计算涉及到的两个关键变量：视点和模型的距离 d ，模型的几何误差 GE ，下面我们看看改变这两个值造成的对应效果。

效果

首先是我们拉进与模型的距离时(即 d 减小)，如果当前模型不变(即 GE 不变)，那么 SSE 变大，如果超过了我们设定的 MSSE ，那么就通知引擎去加载更加精细的模型(精细模型的 GE 更小)。反之，如果我们拉远与模型的距离(即 d 变大)， SSE 就变小，引擎就可以考虑是否加载粗糙一点的模型来减小渲染压力(这里不知道 Cesium 怎么做的，表现上看，当距离拉远时，是会把粗糙的模型加载回来的)。

到这里，我们很容易就能解释，为什么有时候我们加载模型到 Cesium ，如果不修改 Cesium 默认的 MSSE (16)，模型就会变得很模糊。因为，刚进去的粗模计算出来的 SSE 小于默认的 MSSE ，这样就不会触发加载更精细模型的逻辑。

viewer.scene.primitives.add(
  await Cesium3DTileset.fromUrl(url, {
    // default: 16
    maximumScreenSpaceError: 1,
  })
);

屏幕空间误差

问题

概念

计算

效果

参考链接