三角形重心坐标的应用

前言

如何在三角形内部，进行任何属性的插值？或者说，如果知道三角形三个顶点对应属性(纹理，法向量和颜色等)的坐标，如何平滑的得到三角形内部任何一个点对应的属性坐标？

好了， 重心坐标(Barycentic Coordinates) 就这么被引出来了，它就是用来做三角形内的插值的。在讨论插值之前，我们先来几个问题。

问题

为什么要在三角形内插值？

我们会在三角形的定点上定义各种属性，为了能够平滑地得到三角形内每一个点对应的属性值，我们就需要插值；

我们想要插值什么内容？

顶点对应的属性一般有：纹理坐标、颜色和法向量等，有了这些顶点属性，就可以插值出三角形内每一个点对应的顶点属性。当然还有个骚操作，用重心坐标插值重心坐标(笑死.jpg)；

怎么做插值？

等价于重心坐标怎么算；

三角形的重心坐标

定义

重心坐标是定义在一个三角形上的，如果换了一个三角形，那就是另外一套重心坐标了。如下图所示，在三角形ABC形成的一个平面内，任意一个点 P(x, y) ，都可以表示成 A, B, C 三个顶点的线性组合：

$P = (x, y) = αA + βB + γC$

$α + β + γ = 1$

重心坐标

满足上面两个等式的话， (α, β, γ) 就是点P在三角形ABC构成平面对应的重心坐标系下面的重心坐标(PS: 不要把重心坐标系和点的空间笛卡尔坐标系混了)。

需要注意的是，满足上面两个等式，只能证明点P在三角形ABC所在的平面内，并不能确保点P在三角形ABC内。这也就引出了重心坐标的另外一个作用， 判断平面内一点和平面内三角形的空间位置关系 ：

三个系数都是非负的，点在三角形内；
三个系数中存在负数，点在三角形外；
三个系数中存在一个为0，点在三角形的边上；

(PS: 这里是在系数和为1的前提下判断的，如果系数和不等于1，就代表该点不和三角形处于同一个平面)

根据上面两个等式，很容易知道三角形每个顶点在重心坐标系下的重心坐标。 A, B, C 三点对应的重心坐标分别为：

$A_{barycenticCoord} = (1, 0, 0)$

$B_{barycenticCoord} = (0, 1, 0)$

$C_{barycenticCoord} = (0, 0, 1)$

计算

三角形顶点的重心坐标很容易计算出来，那么P点(PS: P点的空间坐标已知)的的重心坐标如何计算？

三角形平面内所在的任意一点的重心坐标可以的通过下式来进行计算：

$α = \frac{-(x - x_B)(y_C - y_B) + (y - y_B)(x_C - x_B)} {-(x_A - x_B)(y_C - y_B) + (y_A - y_B)(x_C - x_B)}$

$β = \frac{-(x - x_C)(y_A - y_C) + (y - y_C)(x_A - x_C)} {-(x_B - x_C)(y_A - y_C) + (y_B - y_C)(x_A - x_C)}$

$γ = 1 - α - β$

特别的是，在三角形内的点我们也可以采用向量的叉乘来计算对应面积比，得到该点的重心坐标。如下图所示：

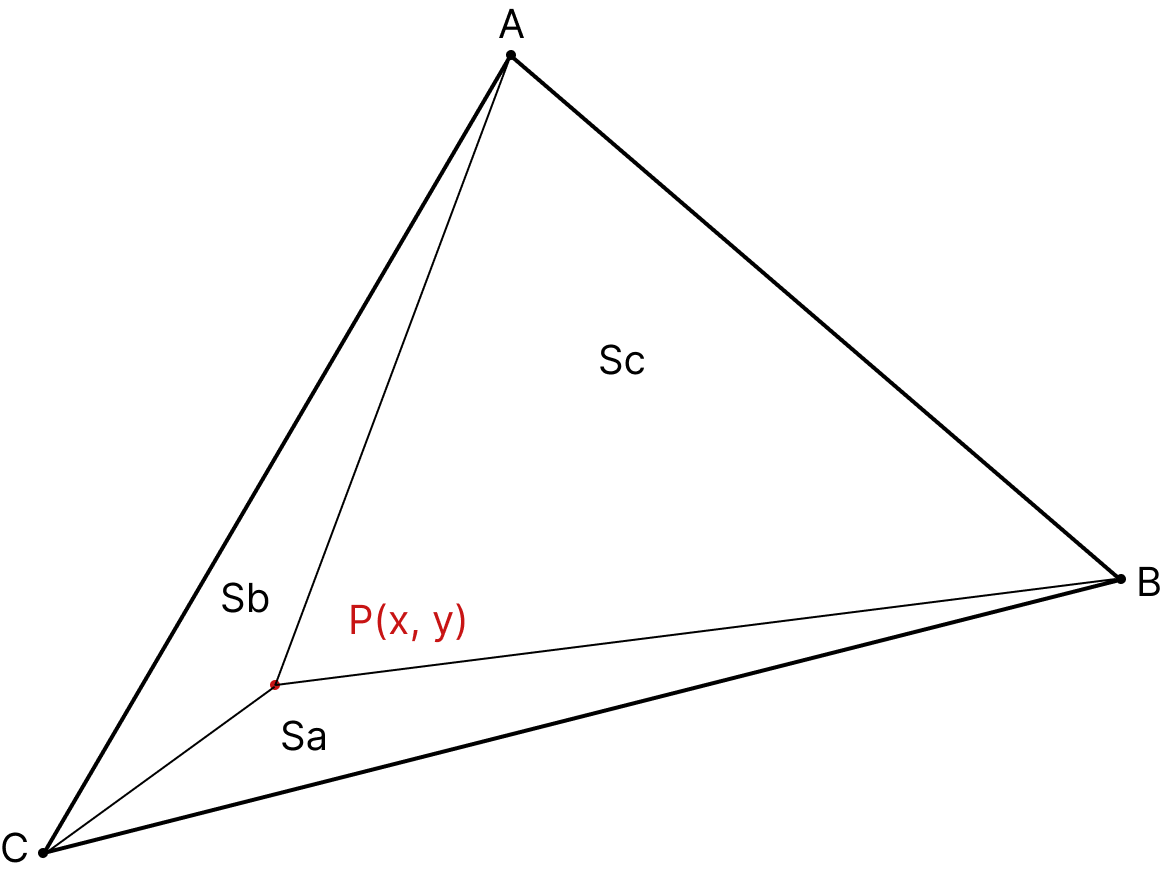
重心坐标计算

$α = \frac{S_a} {S_a + S_b + S_c}$

$β = \frac{S_b} {S_a + S_b + S_c}$

$γ = \frac{S_c} {S_a + S_b + S_c}$

(PS: 计算这块我没有自己推导过这些公式，但是三个未知数，实际上是两个，它们三个满足和为1，根据公式1，很容易可以列两个等式出来，两个等式，两个未知数，emm，合理，能解…)

应用

根据上面的重心坐标计算公式，我们可以得到三角形内任意一点的重心坐标，那么我们就可以根据这些重心坐标去做一些应用。

(PS: 能这么做的原因可以这么理解，三角形内的任意一点的空间坐标满足以重心坐标为参数的三角形三个顶点空间位置坐标的代数和，那么该任意点对应属性也应该满足重心坐标和三个顶点对应属性的代数和。)

颜色插值

如果A点提供红色V_A(1.0, 0.0, 0.0), B点提供绿色V_B(0.0, 1.0, 0.0), C点提供蓝色V_C(0.0, 0.0, 1.0), 那么三角形内任意一点的颜色V就应该等于重心坐标分量乘上对应顶点的颜色值：

$V = αV_A + βV_B + γV_c$

对应的渲染效果如下图所示(网图，是在不想画了):

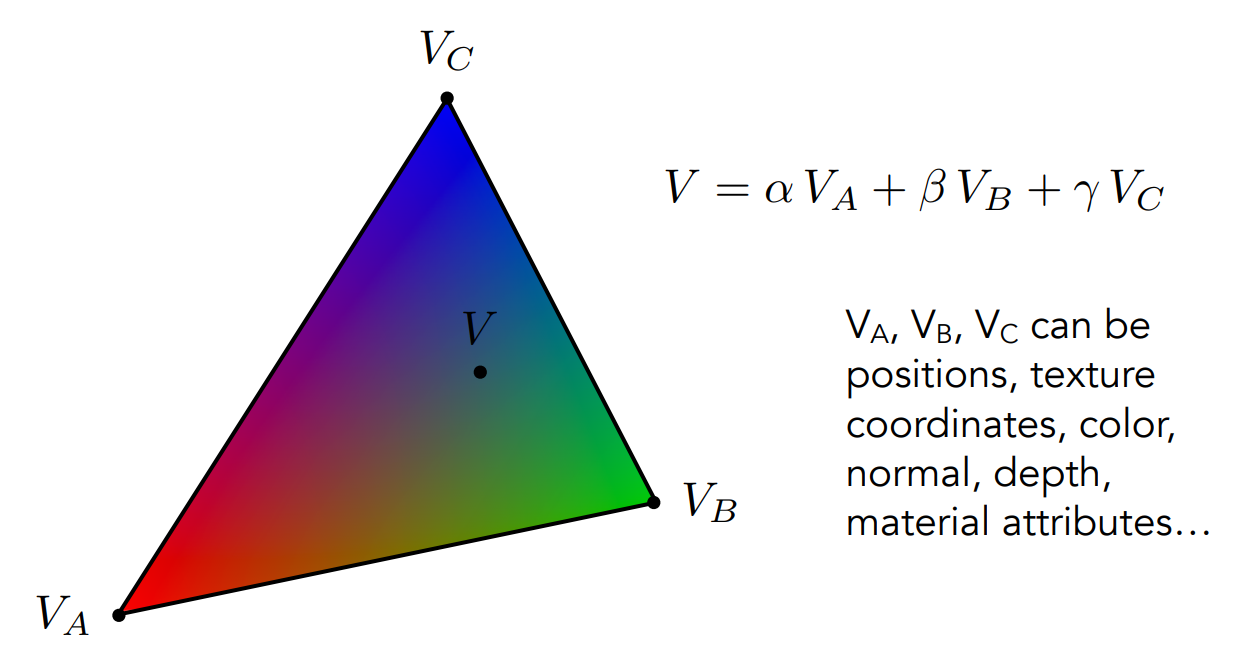
重心坐标颜色插值

我们如果将上面示例的顶点颜色数据传递给渲染管线，渲染出来的图和上图一毛一样，这也从侧面应证了，渲染管线它是按照重心坐标来插值每个像素的颜色的，还不用我们自己去算每个点的重心坐标。

线框模式

该死的WebGL不像OpenGL那样有几何着色器，可以直接支持线框模式。所以在WebGL下面想要展示模型的线框，就需要我们自己去实现，核心就是要 识别三角形的边 。在上文，我们已经说过如何通过重心坐标来判断三角形所在平面内任一点与三角形的位置关系了，当该点的重心坐标存在一个为0(或者说接近某一个阈值，这个阈值其实就是我们设置的线宽)的分量时，代表该点在三角形的边上。现在我们知道怎么判断一个任意点是不是在三角形的边上了，但是有没有发现，任意点的重心坐标我们还没算…

好巧不巧，渲染管线光栅化插值的过程就是利用重心坐标实现的，也就是说渲染管线会计算任意点对应的重心坐标(拿不到)的，我们只需要把三角形的每个顶点的重心坐标传递给渲染管线(这里相当于把重心坐标也当成了一个顶点属性，类似纹理、颜色和法向量)，它就会根据任意点的重心坐标和三个顶点的重心坐标来做对应的代数和得到该点的重心坐标(相当于变相拿到了)。

有没有觉得上面那段话很搞笑，我再多嘴解释一下，因为我们拿不到渲染管线计算出来的重心坐标，所以我们需要传进去三个顶点的重心坐标去拿到任意点的重心坐标…

上面是我在WebGL实现线框模式过程中的理解，具体怎么实现线框可以看参考连接的第三条。

注意

重心坐标有个问题：投影变化不能保证重心坐标的不变。

想想也是，空间中的一个三角形在投影后可能外观都发生了改变，所以对应的重心坐标可能也发生了改变。所以，这里要特别注意的是 任意点Z值的内插 是如何进行的。并不是投到屏幕以后，计算该三角形的重心坐标再去根据三个顶点的深度去内插，而是先根据屏幕坐标反投影回到三维坐标中(PS: 因为该任意点的深度还不知道，所以只能得到该任意点的XY信息，但是三角形所在的平面是确定的，且有XY就可以计算出对应的重心坐标)，根据反投影得到的XY计算出真正的重心坐标，再去和三个顶点进行坐标插值得到真正的深度值。

是不是全是细节，当初看视频完全没有get到…